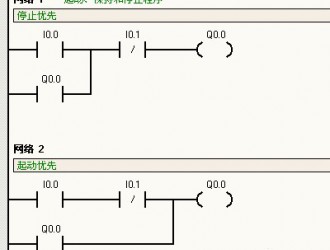
首论代入定理
一条逻辑等式两端所包含之某一变量(仅使用逻辑符号构成的等式),在其所有可能出现的位置均代入换为另一变量后,等式依然应保持成立。
继提反演定理
对于一个由逻辑符号构建而成的函数Y,可通过以下步骤进行转换:
首先,将所有的“.”替换为“+”,再将“+”替换为“.”,接着将“0”替换为“1”,最后将“1”替换为“0”;其次,将原变量转换为反变量,同时将反变量转换回原变量;如此便可得出函数Y的反函数Y'(又称为补函数)。
需特别留意两点:1. 在执行上述操作时,务必遵循“先括号内计算,再进行乘法运算,最后进行加法运算”的运算优先级顺序;
2. 对于不属于单个变量之上的反号,应予以保留,不得随意更改。
再谈对偶定理
对于一个由逻辑符号构建而成的函数Y,可通过以下步骤进行转换:
首先,将所有的“.”替换为“+”,再将“+”替换为“.”,接着将“0”替换为“1”,最后将“1”替换为“0”;其次,将原变量转换为反变量,同时将反变量转换回原变量;如此便可得出函数Y的对偶函数YD。
对偶规则:若两个函数相等,那么它们的对偶函数也必定相等。